How to Use The Simplex Method and Dual Simplex Method with CPLEX and Frontline

Table of Contents: Select a Link to be Taken to That Section

Executive Summary

There are several ways of solving a supply chain optimization problem with CPLEX.
These settings are made in both supply planning applications as well as off-the-shelf optimizers.
There is both a simplex method and a duplex method.

Introduction

The solution procedure is the optimization method that is applied. I often describe and differentiate optimizers based upon their objective function. Therefore, optimizers with an objective function of minimizing costs, I call cost optimizers. Those that attempt to reduce inventory at a set service level or maximize service level at a set inventory level are called inventory optimizers.

To read about this type of optimization, see this article.

CPLEX Options

However, something I have discussed significantly less is the optimization solution selected, which is a subset of the optimization method.

There are some methods, but a small number of them are the most popular. For applications like supply planning, the following would apply.

Where this is set in many optimizers is very clear. This is a screenshot of the Solution Methods tab of the SAP SNP Optimizer. The decomposition methods describe how the problem is segmented to improve run times.

More on this topic can be read about in this article.

However, notice the options at the bottom of the screenshot under LP Solution Procedure.

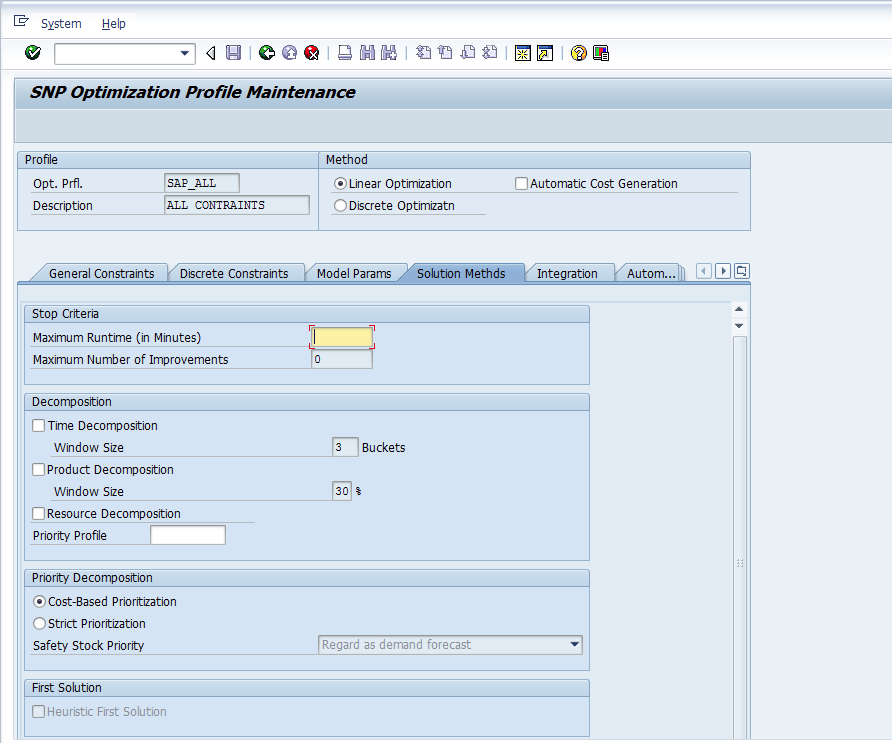
SNP Optimizer Solution Methods Tab

There are three-LP Solution Procedures available to choose from. This is Primal Simplex, Dual Simplex Method, and Interior Point Method, which can be used along with either of the first two options. As the CPLEX solver is actually what is being used, these are the same options provided by CPLEX.

These are described by Wikipedia below:

The IBM ILOG CPLEX Optimizer solves integer programming problems, very large^[2] linear programming problems using either primal or dual variants of the simplex method or the barrier interior point method, convex and non-convex quadratic programming problems, and convex quadratically constrained problems (solved via Second-order cone programming, or SOCP).– Wikipedia

The methods move from the most simple, the Primal Simplex, to the most complex, the Interior Point Method. Simplex is the most commonly used. The simplex method must work with equalities, not inequalities, requiring the introduction of slack variables, which measure the resource’s unused capacity.

Dual Simplex Method

The Dual Simplex method is used for a particular problem where the equality constraints are set up in a specific way. This quote is from Elmer G. Wiens site on operations research:

Like the primal simplex method (or just the simplex), the standard form of the dual simplex method assumes all constraints are <= or =, but places no restrictions on the signs of the RHS (right hand side variables — to read more about right hand side variables see this article. The dual simplex method algorithm consists of three phases.

Phase 0 is identical to Phase 0 of the primal simplex method, as the artificial variables are replaced by the primal variables in the basis. However, the dual simplex method algorithm in Phase 1 searches for a feasible dual program, while in Phase 2, it searches for the optimal dual program, simultaneously generating the optimal primal program. – Elmer G. Weins

The interior-point method solves problems differently from the primal or the dual method simplex. The interior-point begins from the interior of the problem rather than looking across the surface. Where the optimizer starts its search is of great importance as to the final solution it develops.

For instance, in its documentation (a separate optimizer not associated with SAP), MatLab describes how to “change the initial point” of the optimizer in at least one of its online documentation pages.

This is not the only way to change the starting point. The Heuristic First Solution selection will also vary the optimizers’ first point by estimating the best solution with a heuristic before the optimizer begins.

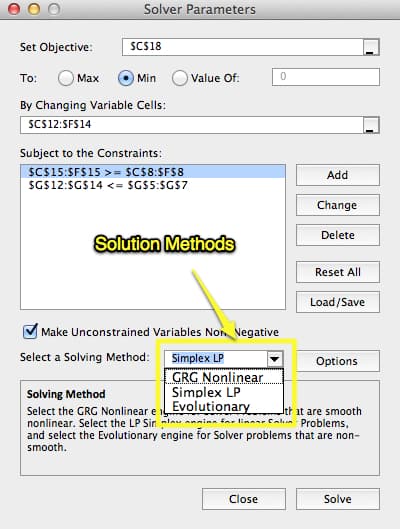
Frontline Solver

The Frontline Solver offers different options, which are listed in the screenshot below:

Something interesting is that Frontline recommends only using the Simplex LP method for non-linear problems. However, CPLEX (which is inside SNP) uses Simplex for non-linear problems (realistic supply planning problems are non-linear).

This discrepancy is something that I will update this post with when I figure out the reason for this.

Go to top

Conclusion

The solution method is always of great emphasis for those using a general solver, which requires that the users get very much into the optimization’s detail. However, on enterprise optimization projects, the optimizer parameter setup’s particulars can often be overlooked due to other issues and distractions.

However, it is interesting and relevant to know what solution methods are being employed and have a good reason for selecting a documented format.